What is Fault Tree Analysis?
Fault Tree Analysis, sometimes abbreviated as FTA, is a top-down deductive approach used to analyze risk and safety issues. It is a methodology used to determine the probability that an unwanted event will occur. The unwanted event is often the failure of a product, system, or process. It can be used for the analysis of highly catastrophic events such as the crash of an airliner, or less critical events, such as a personal drone crashing on landing. The objective of an FTA is to assess the probability, or likelihood, of the undesirable event and then take steps to eliminate, mitigate, or minimize its occurrence to keep failure risk at an acceptable level.
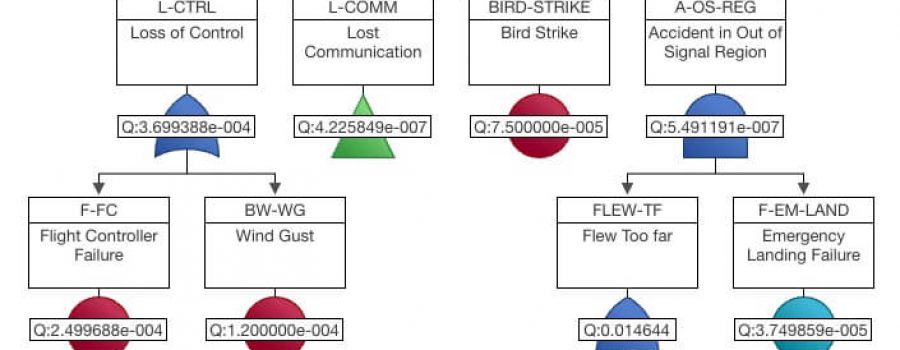
Fault tree analysis begins with the construction of a fault tree diagram. This diagram is a visual representation of events using logic symbols and event symbols. The logic symbols, often called gates, allow you to link events together in the fault tree and are represented by Boolean logic gates. The event symbols, often called events, represent hardware failures, software failures, human errors or other lowest level occurrences that alone or in combination can lead to more significant failures.
Analysis starts at the top level, by defining the main undesired event under investigation. The events that could lead to the top event are then delineated and are connected to the top-level event using logic gates that describe the relationship of input event and their outcomes. The process continues until all lowest level events are identified.
In order to analyze the fault tree diagram, Boolean logic is used. The resulting analysis provides an array of important metrics, including the likelihood, or probability, of the top-most undesirable event.
Logic Gates Used in Fault Tree Analysis
In a fault tree diagram, gates are logic symbols that represent events that can be defined by one or more lower level events. Logic gates have a specific symbol associated with them. By consistently using the known logic symbols, fault tree diagrams are easy to read and interpret.
A list of the logic gates commonly used in FTA include:
- AND
- OR
- NOT
- NAND
- NOR
- Exclusive OR (XOR)
- Inhibit
- Priority AND
- Voting
- Remarks
A common way to describe the Boolean algebra underlying logic gates is by using truth tables. Truth tables delineate all possible combinations of the inputs to a gate along with the resulting output. In truth tables, “T” is used to designate “true”, or an indication of 1, on, or occurrence. “F” is used to designate “false”, or 0, off, or the absence of occurrence.
Read on to learn about the symbol, description, and truth table associated with each logic gate. For ease of understanding, the truth tables below define outputs based on two inputs. However, unless otherwise noted, logic gates are not limited to only two inputs when constructing fault tree diagrams.
Detailed Description of Logic Gates
AND Gate
An AND gate is represented by this symbol:
An AND gate is used when the output occurs only if all the inputs occur.
The logic statement of an AND gate is: All events must be TRUE in order for the output to be TRUE.
Example: My text does not send if I cannot connect to my wifi AND there is no cellular signal.
The truth table for the AND gate is:
| Input 1 | Input 2 | Output |
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | F |
OR Gate
An OR gate is represented by this symbol:
An OR gate is used when the output occurs if one of the inputs occurs.
The logic statement of an OR gate is: If at least one input is TRUE, the output is TRUE. If all inputs are FALSE, the output is FALSE.
Example: I lose control of my personal drone if I fly it too far out of wifi range OR if a strong wind gust occurs.
The truth table for the OR gate is:
| Input 1 | Input 2 | Output |
| T | T | T |
| T | F | T |
| F | T | T |
| F | F | F |
NOT Gate
A NOT gate is represented by this symbol:
A NOT gate is used when the output occurs only if the input does not occur. A NOT gate can only have a single input.
The logic statement of a NOT gate is: If the input is TRUE, the output is FALSE. If the input is FALSE, the output is TRUE.
Example: My security alarm will activate if my front door is NOT closed.
The truth table for the NOT gate is:
| Input | Output |
| T | F |
| F | T |
NAND Gate
A NAND gate is represented by this symbol:
A NAND gate is used to indicate the output occurs when at least one of the inputs does not occur. The NAND gate functions as a combination of an AND gate and a NOT gate.
The logic statement for a NAND gate is: If at least one input is FALSE, the output is TRUE.
Example: A boat has two batteries. As long as one is charged, the boat will start. If battery 1 AND battery 2 are discharged, the boat will NOT start.
The truth table for the NAND gate is:
| Input 1 | Input 2 | Output |
| T | T | F |
| T | F | T |
| F | T | T |
| F | F | T |
NOR Gate
A NOR gate is represented by this symbol:
An NOR gate is used when the output occurs only if all the inputs do not occur. The NOR gate functions as a combination of an OR gate and a NOT gate.
The logic statement for a NOR gate is: If one input is TRUE, the output is FALSE.
Example: If I forgot to charge it OR I cannot remember my passcode, I can NOT use my phone.
The truth table for the NOR gate is:
| Input 1 | Input 2 | Output |
| T | T | F |
| T | F | F |
| F | T | F |
| F | F | T |
XOR Gate
An XOR, Exclusive OR, gate is represented by this symbol:
An XOR gate is used when the output occurs if one input does not occur and one does occur.
The logic statement of an XOR gate is: If one, and only one, input is TRUE, the output is TRUE.
Example: With my camera I can filter using either a polarizing filter or a neutral density filter. The image is not filtered properly if I don’t use either, or if I use both together.
The truth table for the XOR gate is:
| Input 1 | Input 2 | Output |
| T | T | F |
| T | F | T |
| F | T | T |
| F | F | F |
Inhibit Gate
An Inhibit gate is represented by this symbol:
An Inhibit gate is used when the output occurs only if all the inputs occur and the input condition is met.
The logic statement of an Inhibit gate is: If all inputs and the input condition are TRUE, the output is TRUE.
Example: If there is a power outage (conditioning event), I cannot use my laptop if my battery is drained and my UPS fails.
The truth table for the Inhibit gate is:
| Input 1 | Input 2 | Conditioning Event | Output |
| T | T | T | T |
| T | T | F | F |
| T | F | T | F |
| T | F | F | F |
| F | T | T | F |
| F | T | F | F |
| F | F | T | F |
| F | F | F | F |
Priority AND Gate
A Priority AND gate is represented by this symbol:
A Priority AND gate is used when the output occurs only if all the inputs occur in a particular order.
The logic statement of a Priority AND gate is: All events must be TRUE in order for the output to be TRUE, and the events must occur in order.
Example: My oven will overheat if the oven is turned on and then the temperature sensor fails.
The truth table for the Priority AND gate is:
| Input 1 | Input 2 | Output |
| T, occurred first | T, occurred second | T |
| T, occurred second | T, occurred first | F |
| T | F | F |
| F | T | F |
| F | F | F |
Voting Gate
A Voting gate is represented by this symbol:
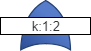
A Voting gate is used when the output occurs only if a set number of inputs occur. Voting gates are designated with the number of required inputs and total inputs, such as 2:3, where 2 of the 3 inputs must occur for the output to occur. If the required number of inputs is equal to 1, a Voting gate is equivalent to an OR gate, since only 1 input is required for the output to occur. If the required number of inputs is equal to the total number of inputs, a Voting gate is equivalent to an AND gate, since all inputs much occur for the output to occur.
The logic statement of a Voting gate is: The output is TRUE only if the required number of inputs is TRUE.
Example: A boat has 3 engines. If 2 of the 3 are on, maximum speed can be attained.
The truth table for the 2:3 Voting gate is:
| Input 1 | Input 2 | Input 3 | Output |
| T | T | T | T |
| T | T | F | T |
| T | F | T | T |
| T | F | F | F |
| F | T | T | T |
| F | T | F | F |
| F | F | T | F |
| F | F | F | F |
Remarks Gate
Fault tree software tools may utilize a Remarks gate for the purposes of adding comments to a diagram or for managing tree layout. There is no logic associated with a Remarks gate, it is simply treated as a pass-through when calculations are performed. In Relyence, the Remarks gate symbol is:
The Transfer Gate
Many fault tree diagramming tools also use a Transfer gate. The symbol for a transfer gate may vary. There is no logic associated with a Transfer gate. The symbol used in Relyence Fault Tree for a Transfer gate is:
A Transfer gate can be used break up large fault tree diagrams into subdiagrams for organization and ease-of-use. The Transfer gate represents a link to another complete fault tree diagram that is a child of the parent diagram.
A Transfer gate can also be used for representing repeated logic in a diagram. For example, there may be multiple places where a particular event and its branch appear in a diagram. You can break out this event and its branch into a sub-diagram and then link to that sub-diagram using a Transfer gate in your main fault tree.
Event Types Commonly Used in Fault Tree Analysis
Along with logic gates, the other elements included in fault tree diagrams are events. Events are the lowest level items in a fault tree diagram. They represent the events that occur that lead up to higher level gates, and ultimately to the top-level gate. Events often have a probability of occurrence associated with them. As event probabilities propagate up the diagram, the probability of all the intermediate levels and the top-level gates can be determined.
A list of the event types commonly used in FTA include:
- Basic
- House
- Undeveloped
- Conditioning
- Repeat
Details of Event Types
Basic
The symbol for a Basic event is:
A Basic event is the lowest level in a fault tree branch, indicating no further breakdown is possible. A Basic event terminates a fault tree branch. For example, Basic events can be hardware failures, human errors, process failures, software failure, or any type of system failure.
House
The symbol for a House event is:
A House event is used to allow turning an event off and on. It allows the probability of the event to be set to 0 (will not occur) or 1 (will occur). Typically, House events are used to allow portions of a fault tree to be included or not included in analysis. It can aid in analyzing the effects of individual branches of a fault tree.
Undeveloped
The symbol for an Undeveloped event is:
An Undeveloped event is similar to a basic event in that it is the lowest level item in a fault tree. However, the Undeveloped event indicates that the event could be further refined and broken down.
For example, an Undeveloped event may be used to indicate that though further resolution is possible, it is not important for the analysis, or does not have an impact on the resulting analysis.
An Undeveloped event could also be used to indicate that further resolution will be done in the future, and the Undeveloped event is a placeholder until that time.
Conditioning
The symbol for a Conditioning event is:
The Conditioning event is always used in conjunction with Inhibit gates. The Conditioning event is the event which must occur in order for the Inhibit gate to possibly occur.
Repeat
The symbol for a Repeat event is the same as a Basic event. In Relyence Fault Tree, a Repeat event is designated by a different color than a Basic event:
A Repeat event is used to represent the same Basic event in multiple locations in the fault tree diagram. Repeat events allow for more organized and efficient analysis.
Conclusion
If you are interested in learning more about fault tree analysis, check out our informative “Answering the 5 W’s of Fault Tree Analysis” blog post.
Learn more about Relyence Fault Tree, our best-in-class fault tree tool for risk and safety assessment or sign up today for your own no-hassle free trial. Feel free to contact us to discuss your needs or schedule a personal demo today.
